Dijkstra算法原理及證明 人工智能理論與算法軟件開發
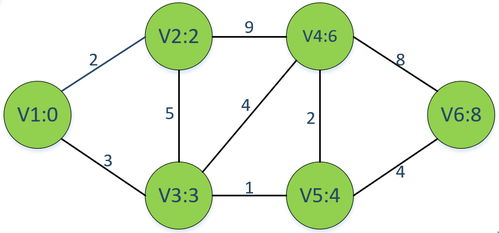
Dijkstra算法是圖論中的一種經典最短路徑算法,廣泛應用于人工智能、網絡路由和軟件開發等領域。它由荷蘭計算機科學家Edsger W. Dijkstra于1956年提出,旨在解決帶權有向圖或無向圖中單源最短路徑問題。本文將詳細介紹Dijkstra算法的原理、證明過程,并探討其在人工智能理論與算法軟件開發中的實際應用。
一、Dijkstra算法的原理
Dijkstra算法基于貪心策略,通過逐步擴展最短路徑樹來尋找從源點到其他所有節點的最短路徑。其核心思想是維護一個距離數組,記錄源點到每個節點的當前最短距離,并通過優先隊列(如最小堆)選擇未訪問節點中距離最小的節點進行松弛操作。
算法步驟如下:
- 初始化:設置源點的距離為0,其他節點的距離為無窮大(表示不可達)。將所有節點標記為未訪問。
- 選擇節點:從未訪問節點中選擇距離最小的節點(記為當前節點)。
- 更新鄰接節點:對當前節點的每個鄰接節點,計算通過當前節點到達該鄰接節點的距離。如果該距離小于已知距離,則更新距離值。
- 標記節點:將當前節點標記為已訪問。
- 重復:重復步驟2-4,直到所有節點均被訪問或目標節點被訪問(在單目標情況下可提前終止)。
算法的時間復雜度取決于數據結構的選擇:使用數組時為O(V^2),使用優先隊列時可優化至O((V+E) log V),其中V為節點數,E為邊數。
二、Dijkstra算法的證明
Dijkstra算法的正確性基于以下關鍵性質:每次選擇的未訪問節點中距離最小的節點,其最短路徑已確定。證明如下:
- 歸納基礎:初始時,源點的距離為0,顯然最短路徑已確定。
- 歸納步驟:假設在前k次迭代中,已訪問的節點集合S中的節點最短路徑已確定。設u為第k+1次迭代中選擇的未訪問節點中距離最小的節點。反證法:假設存在一條從源點到u的更短路徑P,該路徑經過某個未訪問節點v。由于路徑P更短,且邊權非負(Dijkstra算法要求非負權值),路徑P中v到u的段不會減少距離,因此v的距離應小于u的距離,但這與u是未訪問節點中距離最小的選擇矛盾。故假設不成立,u的最短路徑已確定。
該證明依賴于圖的邊權為非負值,如果存在負權邊,Dijkstra算法可能無法得到正確結果,此時需使用Bellman-Ford等算法。
三、在人工智能理論與算法軟件開發中的應用
在人工智能領域,Dijkstra算法常用于路徑規劃、狀態空間搜索和知識推理。例如:
- 機器人導航:在網格或圖中規劃最短路徑,避免障礙物。
- 游戲AI:用于角色移動或資源分配優化。
- 自然語言處理:在圖結構中尋找詞語或概念之間的最短關聯路徑。
在算法軟件開發中,Dijkstra算法是許多系統的基礎組件:
- 網絡路由協議:如OSPF(開放最短路徑優先)使用類似Dijkstra的算法計算路由表。
- 地理信息系統:提供最短駕駛或步行路線。
- 軟件開發工具:集成到圖數據庫或分析庫中,支持復雜查詢。
實際實現時,開發者需注意性能優化,例如使用斐波那契堆等高級數據結構,并處理大數據集下的內存管理。結合A*算法等啟發式方法,可進一步提升效率。
Dijkstra算法以其簡潔性和高效性,成為人工智能和軟件開發中不可或缺的工具。理解其原理與證明,有助于開發者在實際項目中靈活應用并優化算法。
如若轉載,請注明出處:http://www.lqwy888.cn/product/34.html
更新時間:2026-01-10 01:53:24